Содержание | Назад | Далее

9.7. Построение графиков и функций

Рассмотрим построение графика функции на примере функции y = cos² (px),  x Î[0,1]. Для построения графика функции необходимо сначала построить таблицу её значений при различных значениях аргумента с фиксированным шагом. Выберем шаг равным 0,1. Необходимо найти y(0), y(0,1), y(0,2), ... , y(1). С этой целью в диапазон ячеек А1:А11 введем следующие значения переменной x: 0, 0.1, 0.2, …, 1. Выбранные значения образуют арифметическую прогрессию. Заполнение ячеек членами арифметической прогрессии в Excel можно осуществить двумя способами.

Первый способ. В ячейки А1 и А2 вводим первый и второй члены арифметической прогрессии и выделяем эти ячейки. После этого устанавливаем указатель мыши на маркер заполнения выделенного диапазона и протаскиваем его вниз до тех пор, пока не получится числовой ряд нужной длины.

Второй способ. В ячейку А1 вводим первый член арифметической прогрессии. Выбираем команду Правка / Заполнить / Прогрессия и в открывшемся диалоговом окне Прогрессия в группе Расположение устанавливаем переключатель в положение По столбцам, а в группе Тип – в положение Арифметическая . В поле Шаг вводим значение 0.1, а в поле Предельное значение – 1. После нажатия кнопки ОК будет выполнено построение прогрессии.

С помощью команды Правка / Заполнить / Прогрессия можно создавать также геометрические прогрессии.

Ввод формул в ячейку можно производить с клавиатуры или с помощью диалогового окна Мастер функций, вызываемого командой Вставка / Функция или нажатием кнопки панели инструментов Стандартная. Мастер функций содержит список всех встроенных в Excel функций, а также справки по синтаксису функций и примеры их применения.

Выделим ячейку В1 и нажмем кнопку . На экране появится первое диалоговое окно Мастер функций. Это окно содержит два списка: Категория – список, включающий 11 категорий функций, и Функция – список имен функций, входящих в выбранную категорию.

Функция cos относится к категории Математические. Выберем эту функцию и нажмем кнопку ОК. На экране появится второе диалоговое окно Мастер функций. В поле Число введем аргумент функции. В рассматриваемом случае это ПИ()*А1. После нажатия кнопки ОК в ячейку В1 будет введена формула =COS(ПИ()*A1).

Отметим, что при использовании мастера функций перед вводом формулы в ячейку не надо вводить знак «=», т.к. мастер функций введет его сам.

Теперь с помощью клавиатуры добавьте в эту формулу операцию возведения в квадрат. После всех описанных действий в ячейку В1 будет введена формула

=COS(ПИ()*A1)^2.

Для того чтобы завершить процесс табулирования функции, выделим ячейку В1 , установим указатель мыши на маркере заполнения этой ячейки и протащим его вниз до ячейки В11. Для построения графика используется Mастера диаграмм (рис. 19). Вызов мастера диаграмм производится или с помощью команды Вставка / Диаграмма, или нажатием кнопки панели инструментов Стандартная (рис. 19).

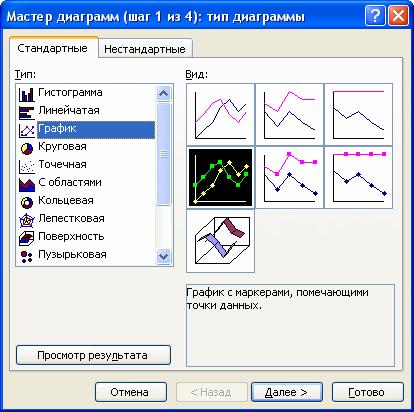
Рис. 19. Первый шаг мастера диаграмм.

Работа с мастером диаграмм осуществляется по шагам. На первом шаге в открывшемся диалоговом окне на вкладке Стандартные выбираем тип диаграммы График, её вид и нажимаем кнопку Далее.

На втором шаге на вкладке Диапазон данных необходимо указать диапазон данных, по которому строится график (рис. 20).

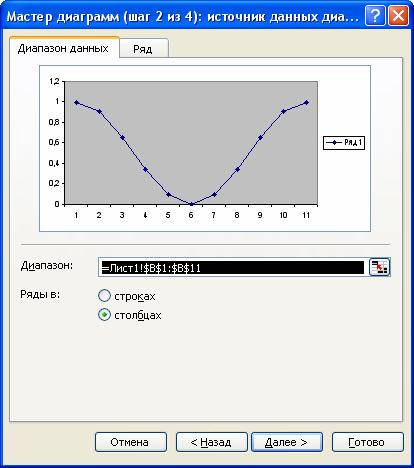
Рис. 20. Второй шаг мастера диаграмм. Вкладка Диапазон данных.

Для этого надо установить переключатель Ряды в столбцах. После этого в окне Диапазон надо указать диапазон данных $B$1:$B$11. Однако проще указать диапазон, протягивая по нему мышь.

На вкладке Ряд в окне Подписи оси Х аналогичным образом надо указать диапазон значений переменной x: =$A$1:$A$11 (рис. 21). Значения из этого диапазона используются в качестве меток оси X. Выполнив эти действия, нужно нажать кнопку Далее.

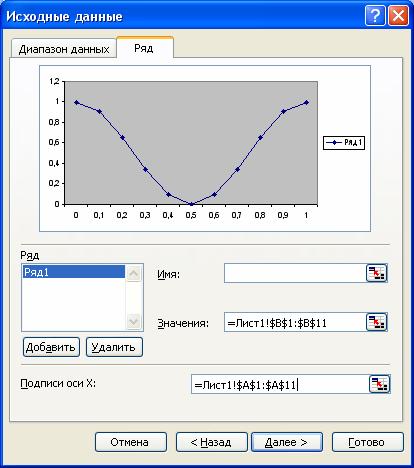
Рис. 21. Второй шаг мастера диаграмм. Вкладка Ряд.

На третьем шаге устанавливаются параметры диаграммы, такие как Подписи данных, Таблица данных, Заголовки, Оси, Линии сетки, Легенда (рис. 22).

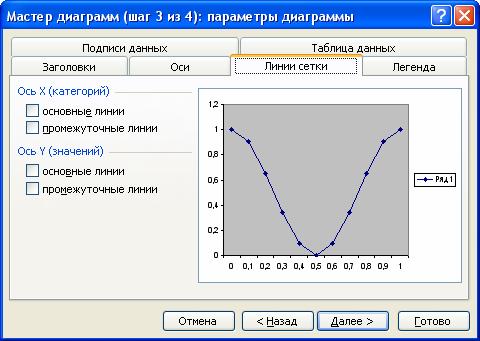
Рис. 22. Третий шаг мастера диаграмм.

На четвертом шаге указывается место размещения диаграммы: на отдельном листе или на имеющемся (рис. 23).

Рис. 23. Четвертый шаг мастера диаграмм.

Построение графика функции завершается нажатием кнопки Готово (рис. 24).

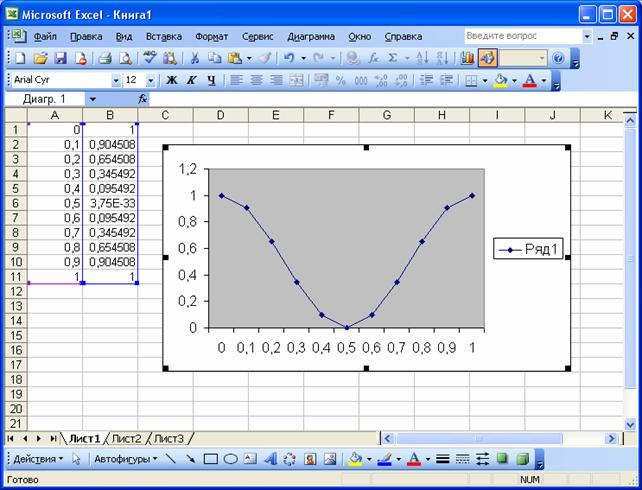
Рис. 24. Результат построения графика функции.

Рассмотрим пример построения графика функции

Этот график строится также, как и предыдущий, за одним исключением – в ячейку В1 вводится формула

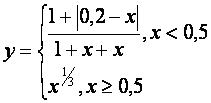
=ЕСЛИ(A1<0,5; (1+ABS(0,2-A1))/(1+A1+A1^2); A1^(1/3)).

Функция ЕСЛИ используется для проверки значений формул и организации переходов в зависимости от результатов проверки.

Синтаксис функции ЕСЛИ

ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь)>

Лог_выражение – любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.

Значение_если_истина – значение, которое возвращается, если лог_выражение имеет значение ИСТИНА.

Значение_если_ложь – это значение, которое возвращается, если лог_выражение имеет значение ЛОЖЬ.

Результат построения графика функции показан на рис. 25.

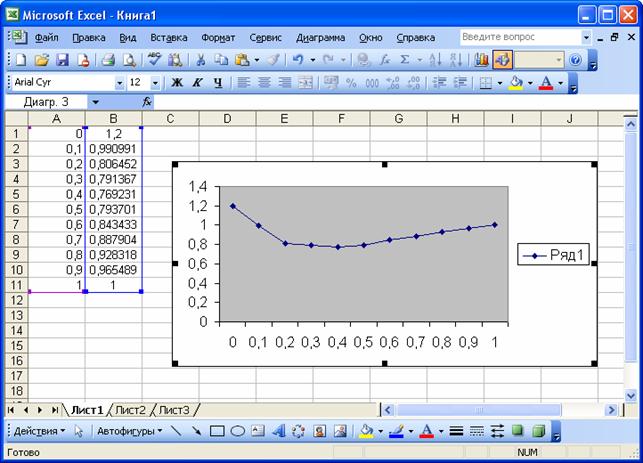
Рис. 25. Результат построения графика функции с помощью функции ЕСЛИ.

Рассмотрим пример построения в одной системе координат графиков следующих двух функций:
 
  y = 2sinx
  z = 3cos2x - sinx
 
при x Î[–3,0].

В диапазон ячеек А2:А17 вводим значения переменной x от –3 до 0 с шагом 0,2. В ячейки В1 и С1 вводим y и z, соответственно. В ячейки В2 и С2 вводим формулы

=2*SIN(A2),

=3*COS(2*A2)–SIN(A2).

Выделим диапазон В2:С2, установим указатель мыши на маркере заполнения этого диапазона и протащим вниз так, чтобы заполнить диапазон В2:С17 .

На первом шаге мастера диаграмм на вкладке Стандартные выберем тип График и вид График с маркерами, помечающими точки данных.

На втором шаге на вкладках Диапазон данных и Ряд указываем диапазон ячеек B1:C17, по которому строятся графики функций, и диапазон A2:A17, по которому стоятся надписи по оси X. Заголовки столбцов Y и Z в ячейках В1 и С1 должны быть включены в диапазон данных, поскольку они используются при построении легенды.

На третьем шаге указываем название диаграммы и надписи на осях. Если необходимо, наносим на график линии сетки, таблицу данных и легенду.

На четвертом шаге указываем место размещения диаграммы. Результат построения приведен на рис. 26.

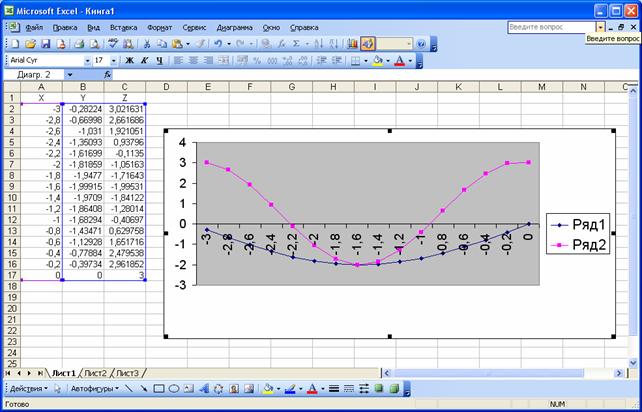
Рис. 26. Результат построения графиков двух функций.

 

Содержание | Назад | Далее