Содержание | Назад | Далее

2. Кодирование данных двоичным кодом

2.1. Двоичное кодирование

Для автоматизации работы с данными разных типов важно уметь представлять их в унифицированной форме. Для этого используется кодирование.

Кодирование – это представление данных одного типа через данные другого типа. Естественные языки – это не что иное, как системы кодирования понятий для выражения мыслей с помощью речи. В качестве другого примера можно привести азбуку Морзе для передачи телеграфных сигналов, морскую флажковую азбуку.

В вычислительной технике используется двоичное кодирование, основанное на представлении данных последовательностью из двух символов: 0 и 1. Эти знаки называются двоичными цифрами, по-английски digit или сокращенно bit (бит).

Одним битом можно выразить два понятия: да или нет, черное или белое, истина или ложь, 0 или 1. Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия:

Тремя битами можно закодировать 8 понятий:

001  011  100  101   110  111.

Увеличивая на единицу количество разрядов, мы увеличиваем в два раза количество значений, которое может быть выражено в данной системе, то есть

где N – количество кодируемых значений;
m – количество двоичных разрядов.

2.2. Кодирование целых чисел

Любое целое число можно представить в виде разложения в полином с основанием два. Коэффициентами полинома являются числа 0 и 1. Например, число 11 может быть представлено в такой форме:

1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰ = 11

Коэффициенты этого полинома образуют двоичную запись числа 11: 1011.

Для преобразования целого числа в двоичный код надо делить его пополам до тех пор, пока в остатке не образуется ноль или единица. Совокупность остатков от каждого деления, записанных справа налево, образует двоичный код десятичного числа.

Для представления целых чисел используется байт, имеющий восемь двоичных разрядов (рис. 2).

Рис. 2. Представление целых чисел.

Первый разряд используется для хранения знака числа. Обычно «+» кодируется нулём, а «–» – единицей. Диапазон представления целых чисел зависит от числа двоичных разрядов. С помощью одного байта могут быть представлены числа в диапазоне от –128 до +127. При использовании двух байтов могут быть представлены числа от –32 768 до +32 767.

2.3. Кодирование вещественных чисел

Существуют два способа представления вещественных чисел в памяти компьютера: с фиксированной точкой и с плавающей точкой.

При представлении вещественных чисел в форме с фиксированной точкой положение десятичной точки в машинном слове фиксировано (рис. 3).

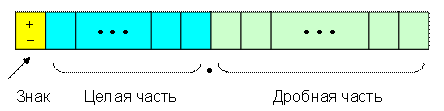
Рис. 3. Вещественное число с фиксированной точкой.

Чаще всего точка фиксируется перед первым разрядом числа (рис.4).

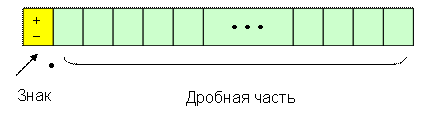
Рис. 4. Вещественное число с точкой перед первым разрядом.

Целое число является частным случаем числа с фиксированной точкой, когда точка фиксирована после последнего разряда.

В форме с плавающей точкой вещественное число х  представляется в виде

где |M|<1 и называется мантиссой, p – целое число, называемое порядком (рис. 5).

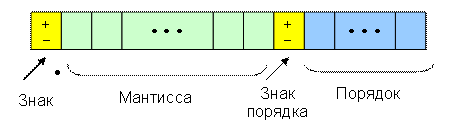
Рис. 5. Вещественное число с плавающей точкой.

Количество позиций, отводимых для мантиссы, определяет точность представления чисел, а количество позиций, отводимых для порядка – диапазон представления чисел.

Обычно мантисса записывается в нормализованном виде, то есть так, чтобы отсутствовали незначащие нули в старших разрядах:

           0.0011101   ненормализованное представление,

           0.1110100   нормализованное представление.

При сложении чисел в форме с плавающей точкой в общем случае нельзя складывать их мантиссы. Если слагаемые имеют разные порядки, то одинаковые разряды мантиссы будут на самом деле изображать разные разряды числа. Поэтому при сложении чисел необходимо предварительно выровнять их порядки, то есть числу с меньшим порядком приписать порядок второго числа и соответствующим образом изменить мантиссу

2.4. Кодирование текстовых данных

Если каждому символу алфавита сопоставить целое число, то можно с помощью двоичного кода кодировать текстовые данные. Восьми двоичных разрядов достаточно для кодирования 256 различных символов. Этого хватает, чтобы закодировать все строчные и прописные буквы английского или русского алфавита, а также знаки препинания, цифры, символы основных арифметических операций и некоторые специальные символы, например «%».

Технически это просто, но существуют организационные сложности. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это трудно осуществить из-за использования различных символов в национальных алфавитах. Сейчас по ряду причин наибольшее распространение получил стандарт США ANСII (American National Code for Information Interchange) – Американский национальный код для обмена информацией. В системе кодирования ANСII закреплены две таблицы кодирования: базовая со значениями кодов от 0 до 127 и расширенная с кодами от 128 до 255.

Коды от 0 до 31 базовой таблицы содержат так называемые управляющие коды, которым не соответствуют символы языка. Они служат для управления устройствами ввода-вывода. Коды с 32 по 127 служат для кодирования символов английского алфавита, знаков препинания, цифр и некоторых других символов. Расширенная таблица с кодами от 128 до 255 содержит набор специальных символов.

Аналогичные системы кодирования разработаны и в других странах. В России большое распространение имеет код КОИ-8.

Трудности создания единой системы кодирования текстовых данных связаны с ограниченным набором кодов (256). Если кодировать символы не 8-разрядными двоичными числами, а 16-разрядными, это позволит иметь набор из 65 536 различных кодов. Этого достаточно, чтобы в одной таблице разместить символы большинства языков. Такая система кодирования называется Unicode – универсальный код. Переход к этой системе долго сдерживался из-за недостатка памяти компьютеров, так как в системе Unicode все текстовые документы становятся вдвое длиннее. В настоящее время технические сложности преодолены и происходит постепенный переход на универсальную систему кодирования.

Общепринятым сегодня считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета. При этом для кодирования яркости любой точки достаточно 8-разрядного двоичного числа.

Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на три основных – красный, зелёный и синий. Для кодирования яркости каждой составляющей используется 256 значений (8 двоичных разрядов). Для кодирования цвета используются 24 разряда. Такая система кодирования обеспечивает представление 16,5 млн различных цветов.

Содержание | Назад | Далее